Linked List (Data Structure)
Definition
A different implementation of the List ADT, where each instance of a Node represents a single element of the list, and LinkedList will represent the list itself.
Node:
from __future__ import annotations
from dataclasses import dataclass
from typing import Optional
@dataclass
class _Node:
"""A node in a linked list.
Instance Attributes:
- item: The data stored in this node.
- next: The next node in the list, if any.
"""
item: Any
next: Optional[_Node] = None # By default, this node does not link to any other node
LinkedList
class LinkedList:
"""A linked list implementation of the List ADT.
"""
# Private Instance Attributes:
# - _first: The first node in this linked list, or None if this list is empty.
_first: Optional[_Node]
def __init__(self) -> None:
"""Initialize an empty linked list.
"""
self._first = None
Traversal
Traversing a linked list can be done with the following patterns: Early return:
curr = my_linked_list._first # 1. Initialize curr to the start of the list.
while curr is not None: # 2. curr is None if we've reached the end of the list.
... curr.item ... # 3. Do something with the current *element*, curr.item.
curr = curr.next # 4. "Increment" curr, assigning it to the next node.
Examples:
Getting the $i$th index of a LinkedList:
Early return loop pattern
class LinkedList:
def __getitem__(self, i: int) -> Any:
"""..."""
# Version 1
curr = self._first
curr_index = 0
while curr is not None:
if curr_index == i:
return curr.item
curr = curr.next
curr_index = curr_index + 1
# If we've reached the end of the list and no item has been returned,
# the given index is out of bounds.
raise IndexError
Other version:
class LinkedList:
def __getitem__(self, i: int) -> Any:
"""... """
# Version 2
curr = self._first
curr_index = 0
while not (curr is None or curr_index == i):
curr = curr.next
curr_index = curr_index + 1
assert curr is None or curr_index == i
if curr is None:
# index is out of bounds
raise IndexError
else:
# curr_index == i, so curr is the node at index i
return curr.item
assertis used to indicate what we know to be true after the loop ends__getitem__is a special method called automatically by the Python interpreter when we use square bracket notation for sequence indexing/dictionary key lookup.
Mutation
Append
class LinkedList:
def append(self, item: Any) -> None:
"""..."""
new_node = _Node(item)
if self._first is None:
self._first = new_node
else:
curr = self._first
while curr.next is not None:
curr = curr.next
# After the loop, curr is the last node in the LinkedList.
assert curr is not None and curr.next is None
curr.next = new_node
with the implementation of ths method, we can now write the initialiser for
LinkedList, albeit an inefficient one:
from typing import Iterable
class LinkedList:
def __init__(self, items: Iterable) -> None:
"""Initialize a new linked list containing the given items.
"""
self._first = None
for item in items:
self.append(item)
This is $\Theta(n^2)$, and it is possible to do it in $\Theta(n)$
Index-Based Mutation
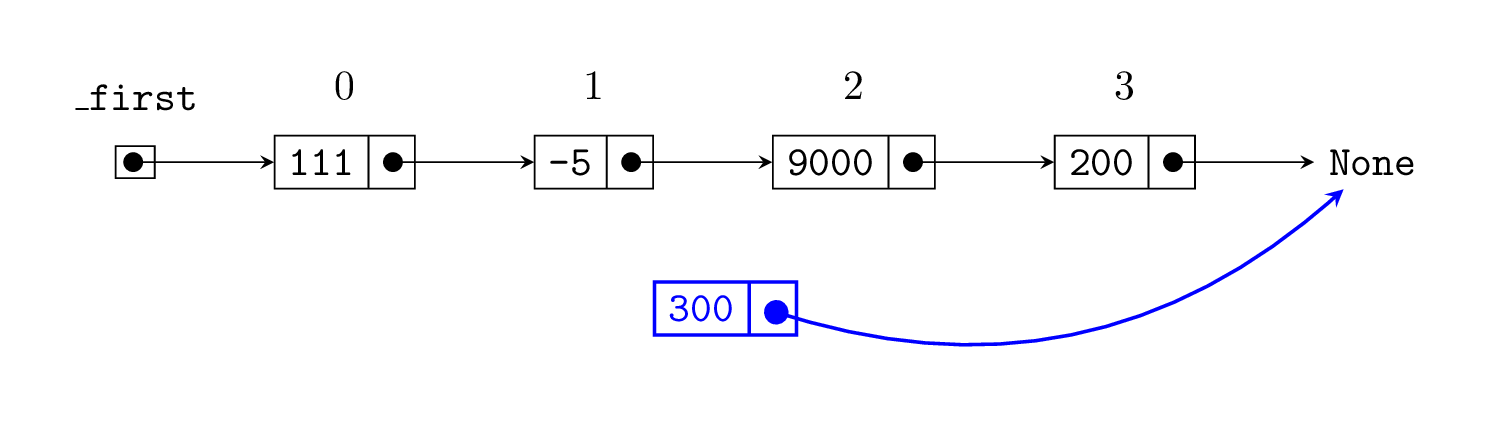
Let's say we want to insert item 300 at index 2
Original list:
 Create a new node (links to None by default):
Create a new node (links to None by default):
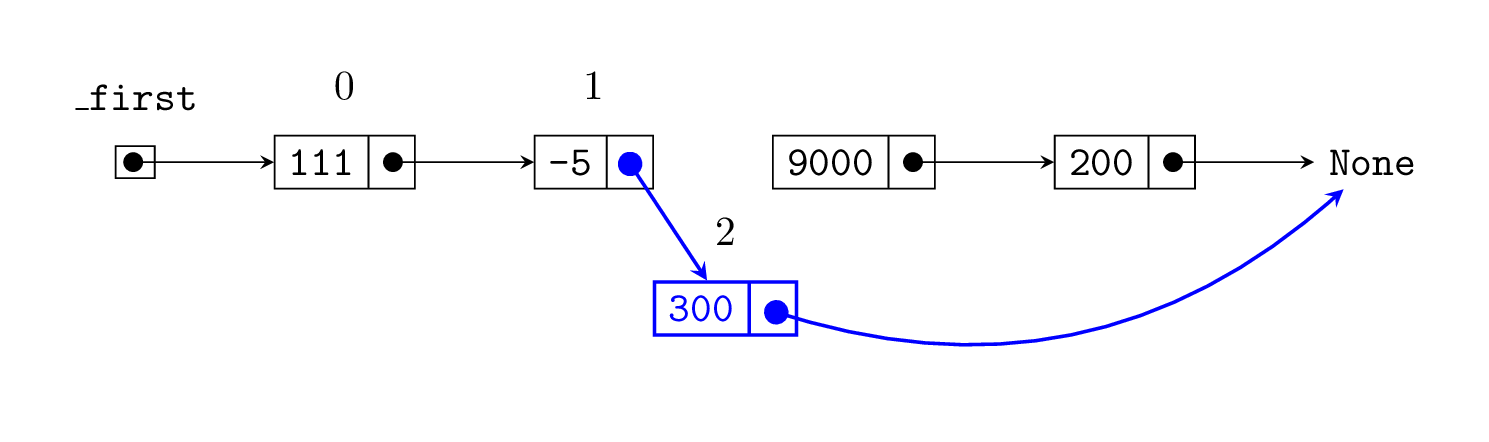
 Modify links (need to modify index-1 node's link):
Modify links (need to modify index-1 node's link):
 Compound Loop Condition:
Compound Loop Condition:
class LinkedList:
def insert(self, i: int, item: Any) -> None:
"""..."""
new_node = _Node(item)
curr = self._first
curr_index = 0
while not (curr is None or curr_index == i - 1):
curr = curr.next
curr_index = curr_index + 1
# After the loop is over, either we've reached the end of the list
# or curr is the (i - 1)-th node in the list.
assert curr is None or curr_index == i - 1
if curr is None:
# i - 1 is out of bounds. The item cannot be inserted.
raise IndexError
else: # curr_index == i - 1
# i - 1 is in bounds. Insert the new item.
new_node.next = curr.next
curr.next = new_node
Early Return: #todo
Running-Time Analysis
Running time for built-in Python list class:
| Operation (assuming $0 \le i < n$) | Running time |
|---|---|
lst[i] | $\Theta(n)$ |
lst.insert(i, element) | $\Theta(n-i)$ |
lst.remove(i) | $\Theta(n-i)$ |
Insert
Case 1: Assume i==0. The if branch executes, taking constant time. 1 step.
Case 2: Assume i > 0.
- The first two statements take constant time. 1 step.
- Statements after while all take constant time. 1 step.
- The statements iterates until it either reaches the end
curr is Noneor the correct indexcurr_index == i -1- The first case takes $n$ iterations, since
curradvances by one_Nodeeach iteration - The second case takes $i-1$ iterations, since
curr_indexstarts at 0 and increases by 1 each iteration
- The first case takes $n$ iterations, since
Hence, total running time = $1 + \min{(n,i-1)} + 1 = \min{(n,i-1)} + 2$ steps
In the first case, we have a running time of $\Theta(1)$, but in the second case, we have a running time of $\Theta(\min{(n,i)})$. The second case would also be $\Theta(1)$ when $i = 0$
The overall running time of LinkedList.insert is $\Theta(\min{(n,i)})$.
| Operation (assuming $0 \le i < n$) | Running time (list) | Running time (LinkedList) |
|---|---|---|
Indexing (lst[i]) | $\Theta(1)$ | $\Theta(i)$ |
| Insert into index $i$ | $\Theta(n - i)$ | $\Theta(i)$ |
| Remove item at index $i$ | $\Theta(n - i)$ | $\Theta(i)$ |